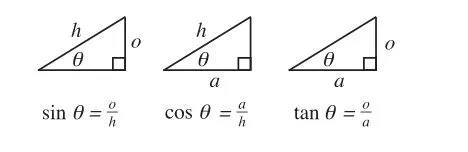Sine, Cosine, Tangent where do they come from
For many students, Mathematics is often a complex subject, however, most students get the above question in their mind.
The Internet helps a lot to find detailed information and fundamentals of the subject matter, hence not repeating it again, giving an absolutely simple answer to this question is very difficult, but the examples given below can give you some insight, if you understand “Fast Fourier transform” in-depth and it’s wide implications and usage, you will start appreciating.
These are ratios that are derived from right-angle triangles
Sine = Opposite/Hypotenuse
Cosine= Adjacent/Hypotenuse
Tangent = Opposite/Adjacent
These ratios are fixed for different angles of any size of right-angle triangles.
Basic few examples of practical use, however, we have practical usage of these in any scientific field.
- Calculate the height of an object and reference your location, for example, you are in one airplane, and there is another airplane you see in the near distance, and you want to know how far it is from you and how elevated it is from you.
- Calculate the distance of a ship from the lighthouse on the beach.
- The velocity of an airplane when you are looking from the plane to the ground.
Abbreviated as sin, cos, tan
From Latin Sinus “fold in a garment, bend, curve.” to Sine
Cosine is the complement of Sine.
Tangent is from the Latin Tangere means to touch.
A detailed explanation can be found below
https://mathisonian.github.io/trig/etymology/